Question

4. Solve the problem.Two cities are 81.4km apart. A police car leaves one city at the same time a firetruck leaves the other city. They are travelling on the same road.Find the speed of the police car in km/h it travels 6,5 km/h faster than the fire truckand if they pass in 14.7 minutes. Assume all values are exactEnter your answer rounded to one decimal place of precision. Do not include units inyour answer.

Answer 1

First of all, we need to make a draw of the problem to understand better:

Both vehicles have a point of interception when pass t=14.7 minutes

The distance between two cities are 81.4 km, then:

`d=81.4\text{ km}`

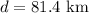
At time of interception t, Police car travels a distance:

`\begin{gathered} v_{police\text{ car}}\cdot t \\ v_{police\text{ car}}\text{ - Sp}eed\text{ of police car } \\ t\text{ = time spent} \end{gathered}`

Similary, Fire truck travels a distance of:

`\begin{gathered} v_{\text{fire truck}}\cdot t \\ v_{\text{fire truck}}\text{ - Sp}eed\text{ of fire truck} \end{gathered}`

But the fire truck is comming from the opposite direction.

When they meet at time t we have the next equation:

`v_{police\text{ car}}\cdot t=d-v_{fire\text{ truck}}\cdot t`

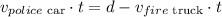
Now we convert time from minutes to hours:

`\begin{gathered} 1\text{ hour = 60 minites} \\ x\text{ hour = 14.7 minutes} \\ x=(14.7\cdot1)/(60)=0.245\text{ hours; then} \\ t=14.7\text{ minutes = 0.245 hours} \end{gathered}`

After that, we make a relation between two speeds, knowing that:

Then:

Finally, we find the speed of car police