Question

You spin once find the p(spin a number less than 3 or a 5) =You spin twice find the p(spin even number and then a number greater than 3) =

Answer 1

Before we begin analyzing the question we were asked, we need to compute the probabilities of getting the individual numbers on the spinner out of a total of 12 slots.

Probability of getting a 1:

There is only a single value of 1, therefore the probability of getting a 1 is:

`P(\text{getting 1)=}(1)/(12)`

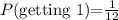
Probability of getting a 2:

There are double values of 2, therefore the probability of getting a 2 is:

`P(\text{getting 2)=}(2)/(12)=(1)/(6)`

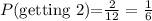
Probability of getting a 3:

There are triple values of 3, therefore the probability of getting a 3 is:

`P(\text{getting 3)=}(3)/(12)=(1)/(4)`

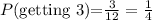
Probability of getting a 4:

There are double values of 4, therefore the probability of getting a 4 is:

`P(\text{getting 4)=}(2)/(12)=(1)/(6)`

Probability of getting a 5:

There are 4 values of 5, therefore the probability of getting a 5 is:

`P(\text{getting 5)=}(4)/(12)=(1)/(3)`

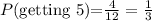
Now that we know the probabilities of getting the individual numbers we can proceed to solving the questions asked.

A number less than 3 or a 5:

The only numbers less than 3 are: 1 and 2.

Since the spinner is spun just once, it means that, if we are to get a number less than 3, then we get either 1 OR 2.

The probability for getting a 1 OR a 2 is:

`\begin{gathered} P(1\text{ OR 2)= P(getting 1) + P(getting 2)} \\ P(1\text{ OR 2) = }(1)/(12)+(1)/(6) \\ P(1\text{ OR 2)=}(1)/(4) \end{gathered}`

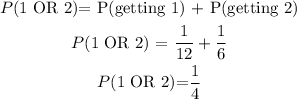
But the question goes on and says in the same trial, what is the possibility of also getting a 5.

This means we can rephrase the question as:

Probability of getting 1 OR 2 OR 5.

Therefore, to fully answer the first question, we say:

`\begin{gathered} P(\text{less than 3 or a 5)=P(1 OR 2 OR 5) = P(1 OR 2) + P(a 5)} \\ P(\text{less than 3 or a 5)=}(1)/(4)+(4)/(12) \\ \\ P(\text{less than 3 or a 5)=}(7)/(12) \end{gathered}`

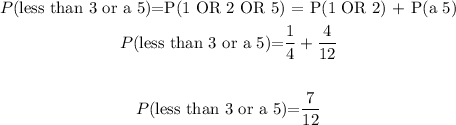
The probability of getting a number less than 3 or a 5 is 7/12

Now for the next question;

Spin Even number and then number greater than 3:

To get an even number you can have only: 2 and 4

The question says you spin twice and asks for the probability in which the first number is even. This means the first number is Either 2 OR 4 not both.

We can compute this probability as:

`\begin{gathered} P(2\text{ OR 4)=P(2) + P(4)} \\ P(2\text{ OR 4) = }(2)/(12)+(2)/(12) \\ \\ \therefore P(2\text{ OR 4)=}(1)/(3) \end{gathered}`

The question also says the second number is a number greater than 3. The only numbers greater than 3 are: 4 and 5.

The second number can be Either 4 OR 5

We can compute this probability as:

`\begin{gathered} P(4\text{ OR 5)=P(4) + P(5)} \\ P(4\text{ OR 5) = }(2)/(12)+(4)/(12) \\ \\ P(4\text{ OR 5)=}(1)/(2) \end{gathered}`

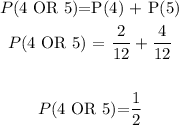
Now that we have both probabilities for the first spin and the second spin, we can therefore calculate for when you get:

Even number AND Number greater than 3

`\begin{gathered} P(2\text{ OR 4) AND P(4 OR 5)= P(2 OR 4) }* P(4\text{ OR 5)} \\ (1)/(3)*(1)/(2)=(1)/(6) \end{gathered}`

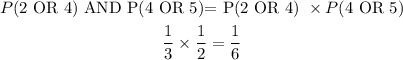
Therefore the probability of getting Even number and number greater than 3 is: 1/6

The final answer is:

#1: 7/12

#2: 1/6