We want to find the function which has a domain of x not equal to -2 and x not equal to 2
For this domain to exists, the function must not exist or be undefined at x = -2 and at x = 2
from the list of option given. Let us look for the option that is undefined at x = -2 and x = 2
Considering the third option
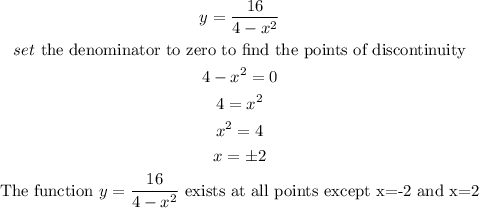
Therefore, the correct option is

;