Question

A rectangular plot of land is 160 feet long and 50 feet wide. How much fencing is needed in order to enclose this plot? What is the total area enclosed by this fencing?

Answer 1

Step-by-step explanation:

Part A:

To figure out the amount of fencing needed to enclose the plot, we will use the formula of the perimeter of a rectangl below

`\begin{gathered} P=2(l+w) \\ where, \\ l=160ft \\ w=50ft \end{gathered}`

By substituting the values, we will have

`\begin{gathered} P=2(l+w) \\ P=2(160ft+50ft) \\ P=2(210ft) \\ P=420ft \end{gathered}`

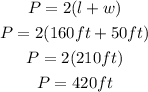
Hence,

The amount of fencing needed to enclose this plot will be

`420ft`

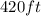
Part A:

The total area nclose by the fencing

This will be calculated using the formula for th area of a rectangle given below as

`\begin{gathered} A=l* w \\ \end{gathered}`

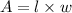
By substituting values, we will have

`\begin{gathered} A=l* w \\ A=160ft*50ft \\ A=8000ft^2 \end{gathered}`

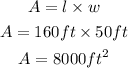
Hence,

The total area enclosed by this fencing is

`8000ft^2`