Question

4. (09.04 MC)Using the following equation, find the center and radius of the circle. You must show all work and calculations to receive credit.X^2 -2x + y^2 - 6y = 26 (10 points)

Answer 1

We have to find the radius and center of the circle from the given equation.

The simplest way to do it is to rearrange the equation in the form:

`(x-a)^2+(y-b)^2=r^2`

which correspond to a circle with center (a,b) and radius r.

Then, we start by writing the equation:

`x^2-2x+y^2-6y=26`

We have to complete the squares for both x and y, so we can do it as:

`\begin{gathered} (x^2-2\cdot1\cdot x+1^2-1^2)+(y^2-2\cdot3\cdot y+3^2-3^2)=26 \\ (x-1)^2-1+(y-3)^2-9=26 \\ (x-1)^2+(y-3)^2=26+1+9 \\ (x-1)^2+(y-3)^2=36 \\ (x-1)^2+(y-3)^2=9^2 \end{gathered}`

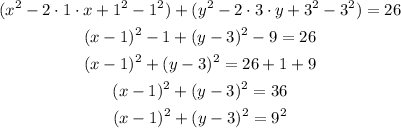
We have arrived to the equation form we needed. In this equation we can see that the center is (1,3) and the radius is r = 9.

Answer: Center is (1,3) and radius is 9.