D is the answer.
The general equation of a line is given as y = mx + c where
m is the gradient, in this case, we can get it at the points (x,y) for 1 and 2 at (0,-4) and (6, 0)
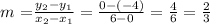
and
c is the intercept on the y-axis clearly seen to cut the y axis at -4
We have the equation to be y = 2x/3 - 4
Thus ratifying our answer.
D is the answer.