Question

write a exponential function to model the situation then find the value of your function after the given amount of time the population of a town is 18,000 and is decreasing at the rate of 2% per year : 6 years

Answer 1

Step-by-step explanation:

The exponential function that models this situation is:

`n(t)=n_0(1-r)^t`

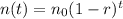
Where n(t) is the amount we want to model the decay, n0 is the initial amout, r is the rate of decay and t is the time in years.

For this particular problem we have n0 = 18,000, r = 0.02 and we have to find n(6)

`\begin{gathered} n(t)=18,000(1-0.02)^t \\ n(t)=18,000*0.98^t \end{gathered}`

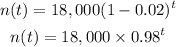
When t = 6:

`n(6)=18,000*0.98^6=15,945.16286`

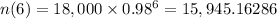
Answers:

• Function:

`n(t)=18,000*0.98^t`

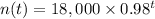
Population after 6 years: 15,945