Question

Find the mean, median, mode, and standard deviation of the given raw data:5 8 10 4 8 10 3 8

Answer 1

We are given the following data

5 8 10 4 8 10 3 8

Mean:

The mean of the data is given by

`mean=(\sum x_i)/(n)`

Where xi are the individual values and n is the number of values in the data set.

`mean=(5+8+10+4+8+10+3+8)/(8)=(56)/(8)=7`

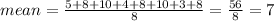
So, the mean of the data set is 7.

Median:

First, we need to arrange the data in ascending order (least to greatest)

3, 4, 5, 8, 8, 8, 10, 10

The median value is given by

`median=((n+1))/(2)=(8+1)/(2)=(9)/(2)=4.5^(th)\;value`

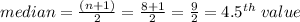
This means that the median is between the 4th and 5th value.

The 4th and 5th both values are 8.

`median=(8+8)/(2)=(16)/(2)=8`

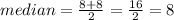
Therefore, the median of the data set is 8

Mode:

The mode is the most repeated value in the data set.

As you can see, the value 8 is most repeated (3 times)

Therefore, the mode of the data set is 8

Standard deviation:

The standard deviation is given by

`SD=\sqrt{\frac{\sum(x_i-\bar{x})}{n-1}}`

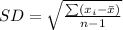
Where x_bar is the mean, and n is the number of values in the data set.

`\begin{gathered} SD=\sqrt{((5-7)^2+(8-7)^2+(10-7)^2+(4-7)^2+(8-7)^2+(10-7)^2+(3-7)^2+(8-7)^2)/(8-1)} \\ SD=2.67 \end{gathered}`

The standard deviation of the data set is 2.67

Summary:

Mean = 7

Median = 8

Mode = 8

Standard deviation = 2.67