Answer:
A. 11.55
Explanation:
Given:
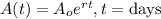
• If the initial amount of substance, A0=1
,
• Then, if after time t, the amount doubles, then A(t)=2
,
• r=6% =0.06
Substitute all these values into the equation.

Next, take the natural logarithm of both sides:
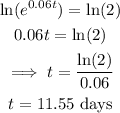
The doubling time (at a rate of 6%) is 11.55 days.