Question

Precalc college levelNot a exam, test, homework, or anything graded Number 25

Answer 1

A. 11.55

Explanation:

Given:

`A(t)=A_oe^(rt),t=\text{days}`

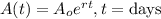
• If the initial amount of substance, A0=1

,

• Then, if after time t, the amount doubles, then A(t)=2

,

• r=6% =0.06

Substitute all these values into the equation.

`\begin{gathered} 2=1e^(0.06t) \\ \implies e^(0.06t)=2 \end{gathered}`

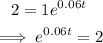
Next, take the natural logarithm of both sides:

`\begin{gathered} \ln (e^(0.06t))=\ln (2) \\ 0.06t=\ln (2) \\ \implies t=(\ln (2))/(0.06) \\ t=11.55\text{ days} \end{gathered}`

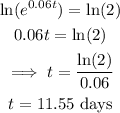
The doubling time (at a rate of 6%) is 11.55 days.