Problem Statement
The question tells us that the number of years new roofs last follows a normal distribution with a mean of 25 and a standard deviation of 5 years.
We are asked to find the following percentages of:
a) between 15 and 35 years.
b) longer than 35 years.
c) less than 20 years
d) between 10 and 35 years.
Method
To solve this question, we need to take note of two formulas. The first is how to calculate the z-score of the individual years, and the other is how to calculate the z-score for a range of years.
Z-score for Individual years:

Z-score for a range of years:
![\begin{gathered} Z_1<p></p><p>Let us apply these formulas to solve the question.</p><p></p><p><strong>Implementation</strong></p><p>a) Between 15 and 35 years:</p><p></p>[tex]\begin{gathered} Z_1=(15-25)/(5) \\ Z_1=-2 \\ \\ Z_2=(35-25)/(5) \\ Z_2=2 \\ \\ \text{Thus, the percentage between 15 and 35 years is given as:} \\ P(-2<p></p><p>b) longer than 35 years:</p><p></p>[tex]\begin{gathered} 35\text{ years is 2 standard deviations away from the mean. Thus from the table given, we can conclude that} \\ \text{the percentage greater than 35 years is:} \\ \\ (100-95)/(2)=2.5\text{ \%} \end{gathered}]()
c) less than 20 years:
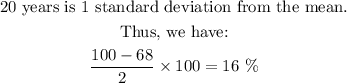
d) between 10 and 35 years:
