We want to find the value that makes
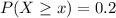
To find it we must look at the standard normal table, using the complementary cumulative table we find that
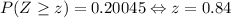
Then, using the z-score we can find the minimum score needed, remember that
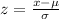
Where
σ = standard deviation
μ = mean
And in our example, x = minimum score needed, therefore
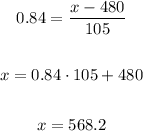
Rounding to the nearest integer the minimum score needed is 568, if you get 568 you are at the top 20.1%.