Question

5#The distribution of scores on a standardized aptitude test is approximately normal with a mean of 480 and a standard deviation of 105. What is the minimum score needed to be in the top 20% on this test? Carry your intermediate computations to at least four decimal places, and round your answer to the nearest integer.

Answer 1

We want to find the value that makes

`P(X\ge x)=0.2`

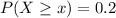
To find it we must look at the standard normal table, using the complementary cumulative table we find that

`P(Z\ge z)=0.20045\Leftrightarrow z=0.84`

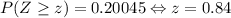
Then, using the z-score we can find the minimum score needed, remember that

`z=(x-\mu)/(\sigma)`

Where

σ = standard deviation

μ = mean

And in our example, x = minimum score needed, therefore

`\begin{gathered} 0.84=(x-480)/(105) \\ \\ x=0.84\cdot105+480 \\ \\ x=568.2 \end{gathered}`

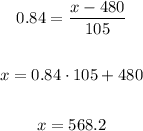
Rounding to the nearest integer the minimum score needed is 568, if you get 568 you are at the top 20.1%.