Question

In a survey, 31 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of $44 and sample standard deviation of $18. Construct a confidence interval at a 98% confidence level.Give your answers to one decimal place.

Answer 1

Given:

sample size (n) = 31

sample mean (bar x) = $44

sample standard deviation = $18

confidence level = 98%

Find: confidence interval

Solution:

To construct a confidence interval, we can use the formula below:

`CI=\bar{x}\pm z((s)/(√(n)))`

where:

bar x = mean

z = z-value at 98% confidence level

s = sample standard deviation

n = sample size

At 98% confidence level, the z-value is 2.326.

Using the formula above, here are our steps:

a. Divide the sample standard deviation $18 by the square root of sample size 31.

`18/√(31)=3.232895436`

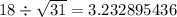
b. Multiply the result to the z-value 2.326.

`3.232895436*2.326=7.519\approx7.5`

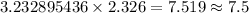
c. Add and subtract 7.5 from the mean of 44.

`\begin{gathered} 44-7.5=36.5 \\ 44+7.5=51.5 \end{gathered}`

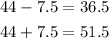
Therefore, the confidence interval at 98% confidence level is from 36.5 to 51.5.