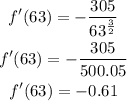Question

A person x inches tall has a pulse rate approximately given by the function y = 610x^-1/2The instantaneous rate of change of the pulse rate for a person that is:(A) 37 inches tall :(B) 63 inches tall:

Answer 1

The pulse rate of a person x inches tall is given by the function:

`y=610x^{-(1)/(2)}`

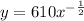
To find the instantaneous rate of change of the pulse rate, we need to find the first derivative of this function and then solve for the x inches tall given.

Follow the next steps:

1. Apply the constant multiple rule of derivatives:

`y^(\prime)=610(d)/(dx)(x^{-(1)/(2)})`

2. Now, to find the derivative apply the power rule of derivatives:

`\begin{gathered} y^(\prime)=610*-(1)/(2)x^{-(1)/(2)-1} \\ y^(\prime)=610*-(1)/(2)x^{-(3)/(2)} \\ y^(\prime)=-\frac{610x^{-(3)/(2)}}{2} \\ y^(\prime)=-\frac{305}{x^{(3)/(2)}} \end{gathered}`

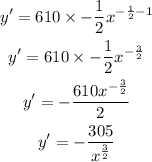
a. A person 37 inches tall will have the following instantaneous rate of change of the pulse rate:

`\begin{gathered} f^(\prime)(37)=-\frac{305}{37^{(3)/(2)}} \\ f^(\prime)(37)=-(305)/(225.1)^{} \\ f^(\prime)(37)=-1.36 \end{gathered}`

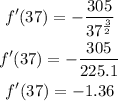
b. A person 63 inches tall will have the following instantaneous rate of change of the pulse rate:

`\begin{gathered} f^(\prime)(63)=-\frac{305}{63^{(3)/(2)}} \\ f^(\prime)(63)=-(305)/(500.05) \\ f^(\prime)(63)=-0.61 \end{gathered}`