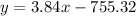Question

Need help with courseReplace 250 with 575 and -3 with -5.

Answer 1

Given

The demand function

`p(x)=(250)/(√(x))-5`

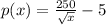
To determine:

a) The revenue function.

b) The marginal revenue.

c) The marginal revenue when x=200.

d) The equation of tangent, and its derivation.

Step-by-step explanation:

It is given that,

`p(x)=(250)/(√(x))-5`

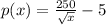
a) The revenue function is given by,

`\begin{gathered} R(x)=x\cdot p(x) \\ R(x)=x*((250)/(√(x))-5) \\ R(x)=250√(x)-5x \end{gathered}`

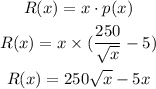
b) The marginal revenue function is,

`\begin{gathered} R^(\prime)(x)=(d)/(dx)(R(x)) \\ =(d)/(dx)(250√(x)-5x) \\ =250*((1)/(2)* x^{-(1)/(2)})-5 \\ =(125)/(√(x))-5 \end{gathered}`

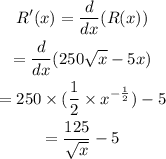
c) The marginal revenue when x=200 is,

`\begin{gathered} R^(\prime)(200)=(125)/(√(200))-5 \\ =(125)/(10√(2))-5 \\ =8.8388-5 \\ =3.8388 \\ =3.84 \end{gathered}`

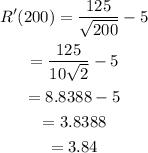
Hence, the marginal revenue is 3.84.

d) Let y=mx+c is the tangent.

Then,

`y=3.84x+c`

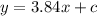
That implies, for y=12.68, and x=200,

`\begin{gathered} 12.68=3.84*200+c \\ 12.68=768+c \\ c=12.68-768 \\ c=-755.32 \end{gathered}`

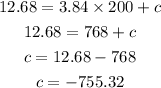
Hence, the equation of tangent is,

`y=3.84x-755.32`