The ramp forms a right triangle like this one:
Where L is the length of the ramp. As you can see L is the hypotenuse of the right triangle and the 29 ft horizontal distance is one of its legs. Here we can use the definition of the cosine of an angle in a right triangle:
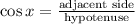
Then for the 30° angle we have:
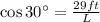
We can multiply both sides of this equation by L and divide by cos30°:
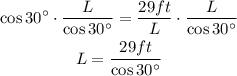
And since:
![\cos 30^(\circ)=\frac{\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/ed11i8lihv8qicqsyf633bwyl6l2d98zq1.png)
We get:
![L=(29ft)/(\cos30^(\circ))=\frac{29ft}{\frac{\sqrt[]{3}}{2}}=\frac{2\cdot29ft}{\sqrt[]{3}}\approx33.49ft](https://img.qammunity.org/2023/formulas/mathematics/college/prayotkwtxrkh4z0wd0r81igxmylm6wl1l.png)
Then the answer is 33.49ft.