Question

You are building a ramp that must cover a horizontal distance of exactly 29 feet. The angle of the ramp from the ground is 30 degrees. Determine the length of the ramp, in feet.

Answer 1

The ramp forms a right triangle like this one:

Where L is the length of the ramp. As you can see L is the hypotenuse of the right triangle and the 29 ft horizontal distance is one of its legs. Here we can use the definition of the cosine of an angle in a right triangle:

`\cos x=\frac{\text{adjacent side}}{\text{hypotenuse}}`

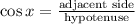
Then for the 30° angle we have:

`\cos 30^(\circ)=(29ft)/(L)`

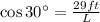
We can multiply both sides of this equation by L and divide by cos30°:

`\begin{gathered} \cos 30^(\circ)\cdot(L)/(\cos30^(\circ))=(29ft)/(L)\cdot(L)/(\cos30^(\circ)) \\ L=(29ft)/(\cos30^(\circ)) \end{gathered}`

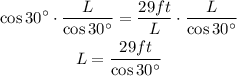
And since:

`\cos 30^(\circ)=\frac{\sqrt[]{3}}{2}`

We get:

`L=(29ft)/(\cos30^(\circ))=\frac{29ft}{\frac{\sqrt[]{3}}{2}}=\frac{2\cdot29ft}{\sqrt[]{3}}\approx33.49ft`

Then the answer is 33.49ft.