Question

The options are relational/irrational and is equal to an integer/has a square root in its denominator

Answer 1

`\text{the quotient }\frac{20}{\sqrt[]{16}}\text{ is an rational number}`

because, the quotient has an integer in its denominator

Step-by-step explanation

A rational number is a number that is expressed as the ratio of two integers

`(p)/(q)`

hence

for

`(20)/(√(16))`

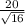
we can solve the root in the denominator, so we have

`\begin{gathered} (20)/(√(16)) \\ \frac{20}{\sqrt[]{16}}=(20)/(4) \end{gathered}`

so, as the number can be expressed as the ratio of two integers ( 20 and 4) we can conclude

`\text{the quotient }\frac{20}{\sqrt[]{16}}\text{ is a rational number}`

because, the quotient has an integer in its denominator

I hope this helps you