Question

Chef Andy tosses an orange in the air, then catches it again at the same height. The orange is in the air for 0.75\,\text s0.75s0, point, 75, start text, s, end text. We can ignore air resistance.What was the orange's velocity at the moment it was tossed into the air?Answer using a coordinate system where upward is positive.Round the answer to two significant digits.

Answer 1

Answer: 3.7 m/s

Explanation: Just is

Answer 2

Given:

Time, t = 0.75

Given that the orange is thrown in the air and is caught again at the same height, let's find the orange's velocity at the moment it was tossed into the air.

Apply the motion equation:

`v=u+at`

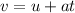
Where:

v is the final velocity

u is the initial velocity

a is the acceleration due to gravity = -9.8 m/s²

t is the time.

For an upward motion, at the maximum height, the final velocity is 0 m/s.

For the first phase(upward motion), the time is half of the total time.

Thus, the time taken to get to maximum height wll be:

`(t)/(2)=(0.75)/(2)=0.375\text{ s}`

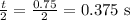
Thus, we now have:

`v=u+at`

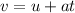
Where:

v = 0 m/s

u is the initial velocity(velocity the moment it was tossed).

a = -9.8t²

t = 0.375 s

Hence, we have:

`\begin{gathered} 0=u-9.8(0.375) \\ \\ u=9.8(0.375) \\ \\ u=3.675\text{ m/s}\approx3.7\text{ m/s} \end{gathered}`

Therefore, the orange's velocity at the moment the orange was tossed into air is 3.7 m/s.

ANSWER:

3.7 m/s