Question

Identify the slope and y-intercept of each linear function's equationslope=-1; y-intercept at 3slope 3, y-intercept at-1slope-3, y-intercept at 11slope 1: y-intercept at-3

Answer 1

We have to identify the slope and y-intercept of each line.

To do that we want to have the following form of the line: y = mx + b, where m is the slope and b is the y-intercept.

a) In the case of the line -x + 3 = y, we can rewrite it as:

`\begin{gathered} -x+3=y \\ y=-x+3 \\ y=(-1)\cdot x+3 \end{gathered}`

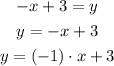
We have made explicit the slope, so we can identify the slope as -1 and the y-intercept as 3.

b) For the line x - 3 = y we can do the same:

`\begin{gathered} x-3=y \\ y=x-3 \\ \Rightarrow Slope:1 \\ \Rightarrow Y-intercept:-3 \end{gathered}`

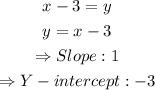
c) For the line y = 3x - 1 we will have:

`\begin{gathered} y=3x-1 \\ \Rightarrow Slope:3 \\ \Rightarrow Y-intercept=-1 \end{gathered}`

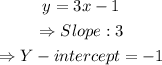
d) For the line y = 1 - 3x we will have:

`\begin{gathered} y=1-3x \\ y=-3x+1 \\ \Rightarrow Slope:-3 \\ \Rightarrow Y-intercept:1 \end{gathered}`

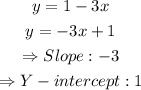
We can then relate the columns as: