We have to identify the slope and y-intercept of each line.
To do that we want to have the following form of the line: y = mx + b, where m is the slope and b is the y-intercept.
a) In the case of the line -x + 3 = y, we can rewrite it as:
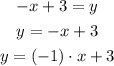
We have made explicit the slope, so we can identify the slope as -1 and the y-intercept as 3.
b) For the line x - 3 = y we can do the same:
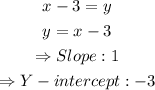
c) For the line y = 3x - 1 we will have:
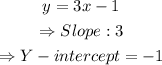
d) For the line y = 1 - 3x we will have:
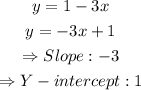
We can then relate the columns as: