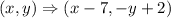Step 1, write the coordinates of the vertices of the triangle GDI
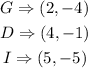
Step 2: Write the coordinates of the vertices of the image G'D'I'
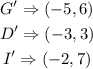
Step 3: Observe the difference in the x-coordinates to obtain the first rule of the transformation
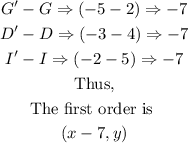
Step 4: Reflect the resulting image over the x-axis
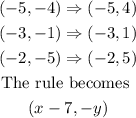
Step 5: Translate the resulting image vertically upward by 2 units
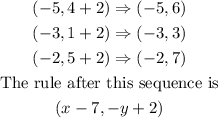
Hence, the rule that represents a series of transformations is given below