Question

2 - 14. What is the equation of the line perpendicular to y - 4 = (x - 6) and passes through the point - (-3,2)? 5 5 - 2 5 = O -2= O A. y-2=-(x + 3) x OB. y + 3 = -(x - 2) (- 2 O c. y - 2 = = (x + 3) OD. y + 3 = (x - 2) 2 2 2 5

Answer 1

The equation of a line that passes through a point is expressed as

`\begin{gathered} y-y_1=m(x-x_1)\text{ ---- equation 1} \\ where \\ m\Rightarrow slope\text{ of the line} \\ y\Rightarrow y-intercept\text{ of the line} \\ (x_1,y_1)\Rightarrow coordinate\text{ of the point through which the line passes} \end{gathered}`

Two lines A and B are said to be perpendicular if the slope of line A is equal to the negative reciprocal of the slope of line B.

Thus, lines A and B are perpendicular if

`m_A=-(1)/(m_B)\text{ ---- equation 2}`

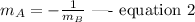
Let the line equation

`y-4=(2)/(5)(x-6)`

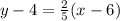
represent the line A.

step 1: Evaluate the slope of line A.

Comparing the equation of line A with equation 1, we can conclude that the slope of the line A is

`m_A=(2)/(5)`

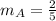
step 2: Evaluate the slope of line B.

Since lines A and B are perpendicular, we have

`\begin{gathered} From\text{ equation 2,} \\ \begin{equation*} m_A=-(1)/(m_B) \end{equation*} \\ where \\ m_A=(2)/(5) \\ thus, \\ (2)/(5)=-(1)/(m_B) \\ cross-multiply \\ -2m_B=5 \\ divide\text{ both sides by -2} \\ (-2m_B)/(-2)=(5)/(-2) \\ \Rightarrow m_B=-(5)/(2) \end{gathered}`

step 3: Evaluate the line B.

Since the line B passes through the points (-3,2), recall from equation 1

`\begin{equation*} y-y_1=m(x-x_1)\text{ } \end{equation*}`

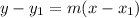
where

`\begin{gathered} x_1=-3 \\ y_1=2 \\ m=m_B=-(5)/(2) \end{gathered}`

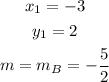
Substitute these values into equation 1.

Thus,

`\begin{gathered} y-2=-(5)/(2)(x-(-3)) \\ \Rightarrow y-2=-(5)/(2)(x+3) \end{gathered}`

Hence, the equation of the line is

`y-2=-(5)/(2)(x+3)`

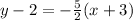
The correct option is A