The domain of a function is the set of all the values that give a defined value for the function.
In the graph, we can see the domain by looking at the x values in which the function is defined.
We have to remember that filled points are consider included and the empty ones are excluded.
As we can see, the left part of the graph starts at point (-3, 9) and it is filled so it includes it. So, the domain "starts" at x = -3, values below it are undefined on the function.
The quadratic part ends at point (4, 16), so at x = 4 and including it. However, the linear part starts at (4, -1), excluding the point, so at the exact point one ends, the other starts, and no x value is left out on the the transition from one part to the other.
Then, the linear part is defined until point (9, -3.xxx). We don't know exactly the value of the y coordinate, bu the x = 9 is enough for use to know that the function is only defined until x = 9, including it.
Putting these together, we see that the function is defined between the x values of -3 and 9, including both, so the domain is:
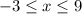
We don't have this exactly alternative because the correct one spliced this interval into the parts of the quadratic and the linear part. So, we can rewrite this domain as:
[tex]-3\le x\le4\, and\, 4
Which corresponds to the third alternative.