To solve for the compound interest semiannually:
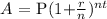
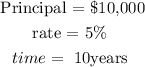
First, convert R as a percent to r as a decimal
r = R/100
r = 5/100
r = 0.05 rate per year,
Then solve the equation for Amount = A, semiannually means twice in a year, n= 2
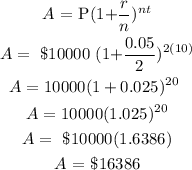
Therefore the annual interest compounded semiannually = $16386.95
Hence the correct answer is Option B