Question

Find the indicated derivative of the function. d3y of y = 2x3 + 2x2 - 5x dx3 - o 6 O 12 O 12x + 6 0 6x +12

Answer 1

The indicated derivative of the function would be 12

Step-by-step explanation:

According to the given data we have the following function:

y=2x^3 + 2x^2 - 5x

To calculate third derivative of the function we would have to make the following calculations:

First find the first derivative of y=2x^3 + 2x^2 - 5x

So:

`(d)/(dx)\mleft(2x^3+2x^2-5x\mright)=6x^2+4x-5`

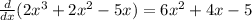
Next, we would have to find the derivative of 6x^2 +4x -5

So:

`(d)/(dx)\mleft(6x^2+4x-5\mright)=12x+4`

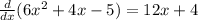
Finally we would have to find the derivative of 12x+4

`(d)/(dx)\mleft(12x+4\mright)=12`

Therefore:

`(d^3)/(dx^3)\mleft(2x^3+2x^2-5x\mright)=12`