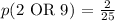Question

In a raffle, a number is picked from 1 to 25. Then another number is picked from 1 to 25.What is the probability that a 2 is drawn on the first pick OR a 9 is drawn on the secondpick? Answer in fraction form. (Hint: Because you could pick a 2 first and a 9 second,these two events are not mutually exclusive.)

Answer 1

If you pick a number from between 1 and 25, it means that the sample space considered is 25 i.e. because there are 25 numbers.

In the first round, a number is picked between 1 and 25, this means that the probability of picking that one number from between 1 and 25 is:

`(1)/(25)`

In the second round, you can pick 1 number from 25 numbers; making the probability of picking the second number:

`(1)/(25)\text{ as well}`

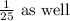
Therefore if you pick 2 in the first round OR you pick 9 in the second round, that means:

`\begin{gathered} P(A\text{ OR B) = P(A) + P(B)} \\ P(2\text{ OR 9) = P(2) or P(9)} \\ \\ We\text{ know that P(2) = P(9) = }(1)/(25) \\ \\ \text{Thus probability of getting a 2 or 9 is:} \\ P(2\text{ OR 9) = }(1)/(25)\text{ + }(1)/(25)=\text{ }(2)/(25) \end{gathered}`

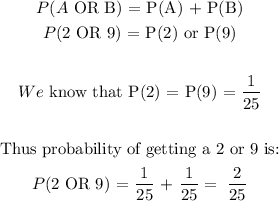
Therefore the final answer is:

`p(2\text{ OR 9) = }(2)/(25)`