Given:
The air pressure at sea level is
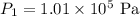
The temperature at sea level is

The air pressure at the final height is
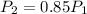
The final temperature is
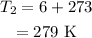
The radius of the bubble at the final height is
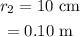
To find:
The initial radius of the bubble
Step-by-step explanation:
We know, for an ideal gas
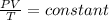
We can write,
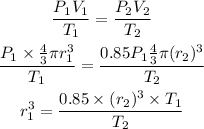
Substituting the values we get,
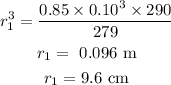
Hence, the radius at sea level was 9.6 cm.