Question

Drooble's best blowing gum is a brand of chewing gum in the wizarding world that allows theconsumer to blow blue bubbles that don't pop for days. Ron is sitting outside chewing on a piece of gum. He blows a bubble that is spherical in shape at sea level (P = 1.01 x 105 Pa) where the temperature is 17°C. After the bubble is released, it begins to float up into the sky to a height where the pressure is 85 percent of the pressure at sea level and it is 6°C cooler. At this height, the bubble has a radius of 10 cm. What is the radius of the bubble that Ron blew at sealevel? The ideal gas constant is 8.31 J/mol*K.

Answer 1

Given:

The air pressure at sea level is

`P_1=1.01*10^5\text{ Pa}`

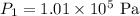
The temperature at sea level is

`\begin{gathered} T_1=17+273 \\ =290\text{ K} \end{gathered}`

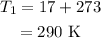
The air pressure at the final height is

`P_2=0.85P_1`

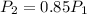
The final temperature is

`\begin{gathered} T_2=6+273 \\ =279\text{ K} \end{gathered}`

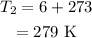
The radius of the bubble at the final height is

`\begin{gathered} r_2=10\text{ cm} \\ =0.10\text{ m} \end{gathered}`

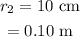
To find:

The initial radius of the bubble

Step-by-step explanation:

We know, for an ideal gas

`(PV)/(T)=constant`

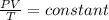
We can write,

`\begin{gathered} (P_1V_1)/(T_1)=(P_2V_2)/(T_2) \\ (P_1*(4)/(3)\pi r_1^3)/(T_1)=(0.85P_1(4)/(3)\pi(r_2)^3)/(T_2) \\ r_1^3=(0.85*(r_2)^3* T_1)/(T_2) \end{gathered}`

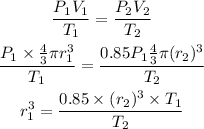
Substituting the values we get,

`\begin{gathered} r_1^3=(0.85*0.10^3*290)/(279) \\ r_1=\text{ 0.096 m} \\ r_1=9.6\text{ cm} \end{gathered}`

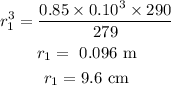
Hence, the radius at sea level was 9.6 cm.