Question

Find the value of c that satisfy the mean value theorem for integrals.

Answer 1

Given

we have a function

`f(x)=-(x^2)/(2)+x-(5)/(2);[-1,0]`

Required

we need to find the value of c that satisfy the mean value theorem for integrals.

Step-by-step explanation

we know that

`f(c)=(1)/(b-a)\int_a^bf(x)dx`

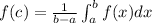
Here a= -1 and b=0

so

`\begin{gathered} f(c)=(1)/(0-(-1))\int_(-1)^0-(x^2)/(2)+x-(5)/(2)dx \\ f(c)=[-(x^3)/(6)+(x^2)/(2)-(5)/(2)x]_(-1)^0=-(19)/(6) \\ i.e.\text{ }-(c^2)/(2)+c-(5)/(2)=-(19)/(6) \\ c^2-2c+5=(19)/(3) \\ 3c^2-6c+15-19=0 \\ 3c^2-6c-4=0 \\ \end{gathered}`

Here c has two values 2.52 and -0.526, but 2.52 does not lie in the interval . So the correct answer is c=-0.526