Given
we have a function
![f(x)=-(x^2)/(2)+x-(5)/(2);[-1,0]](https://img.qammunity.org/2023/formulas/mathematics/college/hhakpe3i1aple2k2topg83j352r8kp466j.png)
Required
we need to find the value of c that satisfy the mean value theorem for integrals.
Step-by-step explanation
we know that
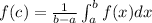
Here a= -1 and b=0
so
![\begin{gathered} f(c)=(1)/(0-(-1))\int_(-1)^0-(x^2)/(2)+x-(5)/(2)dx \\ f(c)=[-(x^3)/(6)+(x^2)/(2)-(5)/(2)x]_(-1)^0=-(19)/(6) \\ i.e.\text{ }-(c^2)/(2)+c-(5)/(2)=-(19)/(6) \\ c^2-2c+5=(19)/(3) \\ 3c^2-6c+15-19=0 \\ 3c^2-6c-4=0 \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dqmsz30xxlno7m8stipsaubb6cofbg4nlq.png)
Here c has two values 2.52 and -0.526, but 2.52 does not lie in the interval . So the correct answer is c=-0.526