ANSWER:
43.68 m/s with a direction of 74.05°
Explanation:
We make the sketch of the situation, just like this:
We can calculate the magnitude of the resulting velocity just like this (By means of the Pythagorean theorem since a right triangle is formed):
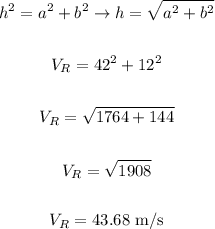
While the direction is calculated as follows (applying the tangent trigonometric ratio):
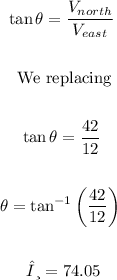
Which means that the resulting velocity is 43.68 m/s with a direction of 74.05°