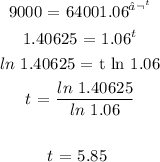Answer:
Step-by-step explanation:
a) Here, we want to get the amount after 2 years
The general formula would be:

where:
A is the amount
P is the principal $6,400
r is the interest rate (6% = 6/100 = 0.06)
n is the number of times interest is compounded yearly (1)
t is the number of years (2)
Substituting the values:
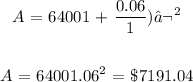
b) Here, we have to calculate t, with A being $9000
We have that as: