Question

Sang invested some money at 7% interest. Sang also invested $193 more than 2 times that amount at 9%. How much is invested at each rate if Sang receives $444.62 in interest after one year? (Round to two decimal places if necessary.)

Answer 1

The interest receive for a simple interest account after t years is given by:

`I=Prt`

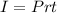
where P is the princial (the amount invested), r is the interest rate in decimal form and t is the time.

Let x be the amount invested in the first account which has a 7% interest rate, the interest given for this account is:

`I_1=0.07x`

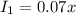
We know that in the second account the investment is 193 more than two times the amount that the investment of the first account, this means that in the second account the principal is 2x+193, then the interest in this account which has a 9% interest rate is:

`\begin{gathered} I_2=0.09(2x+193) \\ I_2=0.18x+17.37_{} \end{gathered}`

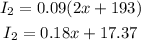
We know that the sum of the interest is $442.62 then we have:

`\begin{gathered} 0.07x+0.18x+17.37=444.62 \\ 0.25x=444.62-17.37 \\ 0.25x=427.25 \\ x=(424.25)/(0.25) \\ x=1709 \end{gathered}`

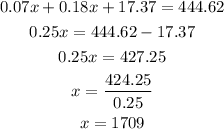
Once we know the value of x we can plug it in the expression for the pincipal in the second account:

`2(1709)+193=3611`

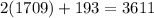
Therefore, Sang invested $1709 in the 7% account and $3611 in the 9% account.