Question

Find the coordinates of R if Q(-1, 3) is the midpoint ofhas coordinates of (5, 6)

Answer 1

The midpoint is given by the following expression:

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

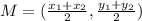
Where:

Therefore:

`(M_x,M_y)=((X_1+X_2)/(2),(y_1+y_2)/(2))`

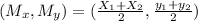
Replacing:

Mx= 5 and My=6

Qx= X1 =-1 and Qy= y1=3

Rx=X2 and Ry= Y2

`(5,6)=((-1+x_2)/(2),(3+y_2)/(2))`

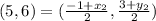
Equating the x component and solving for X2:

`\begin{gathered} 5=(-1+x_2)/(2) \\ 5*2=-1+x_2 \\ 10+1=x_2 \\ x_2=11 \end{gathered}`

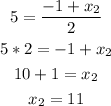
Doing the same with the y component:

`\begin{gathered} 6=(3+y_2)/(2) \\ 6*2=3+y_2 \\ y_2=12-3=9 \\ y_2=9 \end{gathered}`

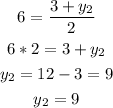
Answer: the coordinates of R are: (X2,Y2) = (11 , 9).