Question

Need help with a equation

Answer 1

Hello there. To solve this question, we'll have to remember some properties about vertical angles.

Given two angles A and B, they are said to be vertical angles if and only if:

That is, their measures are the same.

In this question, we have that the angles A and B have measures respectively equal to:

`m\angle A=\lparen2x-10)^{\circ\text{ }}=m\angle B=\left(x+8\right)^(\circ)`

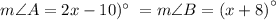
Solving this equation for x:

Subtract x on both sides of the equation. Add 10 in the same manner.

`\begin{gathered} 2x-10-x+10=x+8-x+10 \\ x=18 \end{gathered}`

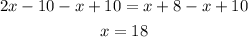
Therefore we have the solution for x.

Now we plug this into A in order to find its measure:

`m\angle A=\left(2\cdot18-10\right)^(\circ)=\left(36-10\right)^(\circ)=26^(\circ)`

This is the answer to this question.