Answer:
490
Step-by-step explanation:
The number of ways or combinations to select x objects from a group of n is equal to
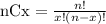
A person has 8 options for movies and he is going to select 4, the number of combinations for movies is
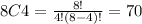
In the same way, the person has 7 options for books and he is going to select 6, so

Then, the total number of combinations for 4 movies and 6 books is calculated as:
70 x 7 = 490 possible combinations
Therefore, the answer is 490 possible combinations