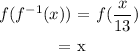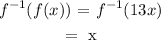Given that the function
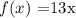
is a one-to-one function,
A) Equation for f⁻¹(x), the inverse function.
From the function f(x), interchange x and f(x).
thus,
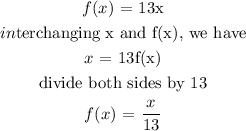
thus, equation for f⁻¹(x), the inverse function is

B) To show that f(f⁻¹(x)) = x and f⁻¹(f(x)) = x
Starting with f(f⁻¹(x)):
Evaluating f(f⁻¹(x)) involves substituting the f⁻¹(x) function into the f(x) function.
In this case, let f⁻¹(x) be z(x).
Thus, we have f(f⁻¹(x)) to be f(z).
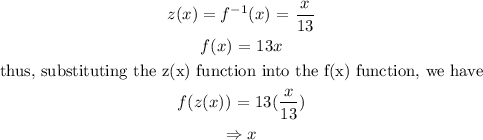
For f⁻¹(f(x)):
Similarly, evaluating f⁻¹(f(x)) involves substituting the f(x) function into the f⁻¹(x) function.
Thus, we have

Hence,