Question

From the top of a building 40 feet above the ground a construction worker locates a rock at a 12° angle of depression how far is the rock from the building around the answer to the nearest foot

Answer 1

Step-by-step explanation:

The question willbe solved using the image below

If 12 degrees is the angle of depression from eye level of the worker, then the vertex angle is complementary to that angle. The vertex angle, the "top" angle of the right triangle is 78 degrees. The height of the triangle is 40 and we are to find the length of the base of the triangle because that length represents how far away the rock is from the base of the building. We have the reference angle as 78, the side across from it (x), and the side adjacent to it (40). That means that we will use the tangent ratio to find the missing side

Hence,

The answer will be calculate below as

`\begin{gathered} tan78^0=(x)/(40) \\ x=40\tan78^0 \\ x=188.18ft \end{gathered}`

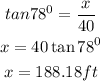
Hence,

The final answer is

`188ft`

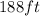
The THIRD OPTION is the correct answer