Given:
Product and quotient rule.
Required:
Explain the product and quotient rule with examples.
Step-by-step explanation:
Product rule:
If two functions are in the multiple forms then the derivative of two functions is given by the formula:
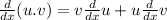
where u = first function and v = second function.
Example

Quotient Rule:
If two functions are given in the quotient form or division form then the derivative of these functions using the quotient rule is given as:
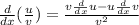
Example:
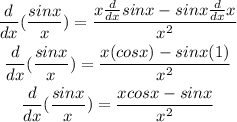
Final Answer:
As explained in the explanation part.