Question

Triangle DEF and triangle CBD are similar right triangles. у 9 B E F 6 5 4 С 2 1 X 2 2 3 4 5 6 7 8 9 -=8 -7 -6 -5 -4 -3 - 1 1-1 D - в 3 5 6 -8 9 Which statement about the slopes of DF and CD is true?

Answer 1

a) DF has the same slope as CD

Step-by-step explanation:

Since the points D, F, and C all belong to the same line, we can say that the slopes of DF and CD are equal.

So, a statement that is true about the slopes of DF and CD is a statement that says that they have the same slope.

The slope of a line can be calculated using the coordinates of two points as:

`m=(y_2-y_1)/(x_2-x_1)`

So, the slope of DF can be calculated by replacing (x2, y2) by F(1, 7) and (x1, y1) by D(-1, -2), so:

`m=(7-(-2))/(1-(-1))=(9)/(2)`

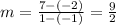
In the same way, the slope of CD can be calculated by replacing (x2, y2) by D(-1, -2) and (x1, y1) by C(0, 4), so: