Question

The ordered pair (5,-3) is a solution to which of the following inequalities?

Answer 1

In order to check if the pair (5, -3) is a solution of each inequation, we need to use the value of x=5 and y=-3 in each inequation and check if the corresponding sentence is true.

For the first inequation, we have:

`\begin{gathered} 4y+2x\le-1 \\ 4(-3)+2(5)\le-1 \\ -12+10\le-1 \\ -2\le-1\text{ (true)} \end{gathered}`

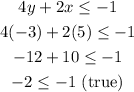
The final sentence is true, so the pair is a solution to this inequation.

For the second inequation, we have:

`\begin{gathered} y\ge-2x+8 \\ -3\ge-2(5)+8 \\ -3\ge-10+8 \\ -3\ge-2\text{ (false)} \end{gathered}`

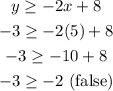
The final sentence is false, so the pair is NOT a solution to this inequation.

For the third inequation, we have:

`\begin{gathered} -2y<3x-9 \\ -2(-3)<3(5)-9 \\ 6<15-9 \\ 6<6\text{ (false)} \end{gathered}`

The final sentence is false, so the pair is NOT a solution to this inequation.

For the fourth inequation, we have:

`\begin{gathered} y-2x>5 \\ -3-2(5)>5 \\ -3-10>5 \\ -13>5\text{ (false)} \end{gathered}`

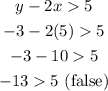
The final sentence is false, so the pair is NOT a solution to this inequation.

So the answer is the first option.