Question

6.1.23 Find the missing angle measure. B А F 500 1299 130° D The measure of the missing angle is (Type an integer or a fraction.)

Answer 1

Given the figure ABCDEF, you can identify that it is an Irregular polygon.

As you can see, this polygon has 6 sides. Then, you can set up that:

`180(n-2)`

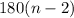
That formula can be used to find the sum of the interior angles of a polygon.

In this case:

`n=6`

Then, you get:

`=180(6-2)=720\degree`

Knowing that the sum of the interior angles of this polygon is 720°, you can set up the following equation:

`x+147\degree+161\degree+50\degree+128\degree+130=720\degree`

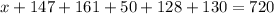
Finally, solving for "x", you get:

`\begin{gathered} x=720\degree-616\degree \\ x=104\degree \end{gathered}`

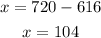
The answer is:

`104\degree`