Question

$3168 is invested in the stock market. Shares in Mazda are bought at $7.20 each and shares in Honda are bought at $4.80 each. The total number of shares bought is 500. How many shares of each stock is purchased?

Answer 1

To answer this question we will set and solve a system of equations.

Let M be the number of shares of Mazda that were bought, and H be the number of shares of Honda. Then we can set the following system of equations.

`\begin{gathered} M+H=500, \\ 7.20M+4.80H=3168. \end{gathered}`

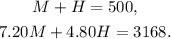
Subtracting M from the first equation we get:

`\begin{gathered} M+H-M=500-M, \\ H=500-M\text{.} \end{gathered}`

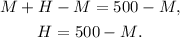
Substituting the above equation in the second one we get:

`7.20M+4.80(500-M)=3168.`

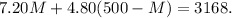
Applying the distributive property we get:

`7.20M+2400-4.80M=3168.`

Adding like terms we get:

`2.4M+2400=3168.`

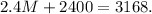
Subtracting 2400 from the above equation we get:

`\begin{gathered} 2.4M+2400-2400=3168-2400, \\ 2.4M=768. \end{gathered}`

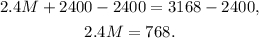
Dividing the above equation by 2.4 we get:

`\begin{gathered} (2.4M)/(2.4)=(768)/(2.4), \\ M=320. \end{gathered}`

Substituting the above equation at H=500-M we get:

`\begin{gathered} H=500-320, \\ H=180. \end{gathered}`

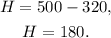
Answer: 320 shares in Mazda and 180 shares in Honda.