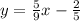Question

Find an equation for the line perpendicular to the line 9x + 5y = 5 having the same y-intercept as 7x - 5y = 2.

Answer 1

To find the equations fo a line, we can use the "slope" and a point contained in the ilne.

For the slope, we will use the first given line:

`9x+5y=5`

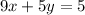
Firstly, let's right it in the standard form, that is, with "y" alone in the left side:

`\begin{gathered} 9x+5y=5 \\ 5y=-9x+5 \\ y=-(9)/(5)x+1 \end{gathered}`

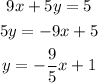
The slope of this line is:

`s_1=-(9)/(5)`

Since the line we want is perpendicular to this first line, we can get the slopeof we need by inverting s1 and changing its sign.

So, the slope of the line we want, s, is:

`s=-(1)/(s_1)=-(1)/(-(9)/(5))=-(-(5)/(9))=(5)/(9)`

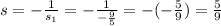
We have found the slope, now we need a point.

For this, we will use the information that it has the same y-intercept as the line:

`7x-5y=2`

The y-intercept is the point there the line intercepts the y-axis, that is, when x = 0. So, to find it, we just put x = 0 and solve for y:

`\begin{gathered} 7\cdot0-5y=2 \\ -5y=2 \\ y=-(2)/(5) \end{gathered}`

Since, our line has the same y-intercept, wecan use this information to complete it.

For now, we only know the slope, so our equation is:

`\begin{gathered} y=sx+a \\ y=(5)/(9)x+a \end{gathered}`

Since the y-intercept is y = -2/5, we can put this and x = 0 to find "a":

`\begin{gathered} -(2)/(5)=(5)/(9)\cdot0+a \\ -(2)/(5)=a \\ a=-(2)/(5) \end{gathered}`

So, the final equation is:

`y=(5)/(9)x-(2)/(5)`