Question

Consider the following functions.f(x) = x^2 + 2x, g(x) = 3x^2 - 1

Answer 1

`\begin{gathered} a)(f+g)(x)=4x^2+2x-1 \\ \text{Domain:(-}\infty,\infty) \\ c)(f-g)(x)=-2x^2+2x+1 \\ \text{Domain:(-}\infty,\infty) \\ e)(fg)(x)=3x^4+6x^3-x^2-2x \\ \text{ Domain}(-\infty,\infty) \\ g)((f)/(g))(x)=((x^2+2x))/((3x^2-1)) \\ \text{Domain:}(-\infty,\frac{1}{\sqrt[]{3}})\cup(\frac{1}{\sqrt[]{3}},\infty) \end{gathered}`

Step-by-step explanation

The domain of a function is the set of all possible inputs for the function.

so

Let

`\begin{gathered} f(x)=x^2+2x \\ g(x)=3x^2-1 \end{gathered}`

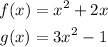
Step 1

a) (f+g)(x)

to add the function , add like terms

`\begin{gathered} f(x)+g(x)=(f+g)(x)=x^2+2x+3x^2-1 \\ (f+g)(x)=x^2+2x+3x^2-1 \\ (f+g)(x)=4x^2+2x-1 \end{gathered}`

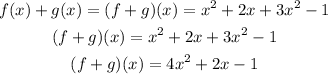
so

`a)(f+g)(x)=4x^2+2x-1`

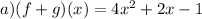
(b) domain of the function:

the domain of a quadratic function f(x) is the set of x -values for which the function is defined,so

`\text{Domain:(-}\infty,\infty)`

Step 2

c) (f-g)(x)

subtract the functions

`\begin{gathered} f(x)-g(x)=(f-g)(x)=x^2+2x-(+3x^2-1) \\ (f-g)(x)=x^2+2x-3x^2+1 \\ (f-g)(x)=-2x^2+2x+1 \end{gathered}`

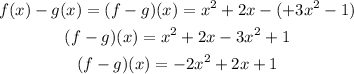
d)Domain:For any linear function the domain and range are always all real numbers

`\mleft(-\infty,\infty\mright)`

Step 3

e) (fg)(x)

`\begin{gathered} f(x)=x^2+2x \\ g(x)=3x^2-1 \\ \text{then} \\ (fg)(x)=(x^2+2x)(3x^2-1) \\ \text{apply distributive property} \\ (fg)(x)=(x^2\cdot3x^2)-(1\cdot x^2)+(2x\cdot3x^2)-(2x\cdot1) \\ (fg)(x)=3x^4-x^2+6x^3-2x \\ \text{reorder} \\ (fg)(x)=3x^4+6x^3-x^2-2x \end{gathered}`

f) again we have a polynomial so, The domain of all polynomial functions is all real numbers:

`\text{ Domain}\mleft(-\infty,\infty\mright)`

Step 4

g) (f/g)(x)

`\begin{gathered} f(x)=x^2+2x \\ g(x)=3x^2-1 \\ \text{then} \\ ((f)/(g))(x)=((x^2+2x))/(\mleft(3x^2-1\mright)) \\ \end{gathered}`

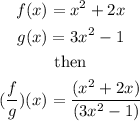
h) domain, we see this function is not definded when the denominator equals zero, we need to find that number

`\begin{gathered} 3x^2-1=0 \\ \text{add 1 in both sides} \\ 3x^2-1+1=0+1 \\ 3x^2=1 \\ \text{divide both sides by 3} \\ (3x^2)/(3)=(1)/(3) \\ x^2=(1)/(3) \\ √(x^2)=\sqrt{(1)/(3)} \\ x=\frac{1}{\sqrt[]{3}} \\ so,\text{ the domain is} \\ (-\infty,\frac{1}{\sqrt[]{3}})\cup(\frac{1}{\sqrt[]{3}},\infty) \end{gathered}`

I hope this helps you