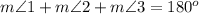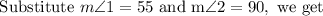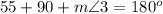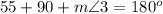Question

Need help on this question, not sure how to do this

Answer 1

Angle 4: 80
Angle 7: 135

In order to find angle 4, we need to find angles 3 and 5 so we can add them all up to 180, because all angles on a straight line must combine into 180. Since AB and CD are parallel to each other, angles 1 and 5 will be congruent because they are corresponding angles. Since we were given that angle 1 is 55, then angle 5 must also be 55. Both pairs of parallel lines form a right angle where they intersect according to angle D, therefore angle 2 must also be a right angle (90). With that knowledge, we can combine angles 1 and 2 and subtract that them from 180 in order to find angle 3, because all angles in a triangle must add up to 180.

180-55-90=45

Now that we know angles 3 and 5, we can do the same thing and subtract them both from 180 to find angle 4.

180-55-45=80

Angle 4 is 80.

To find angle 7, we must find angle 6 and subtract it from 180.

We know from before that angles 1 and 5 are congruent because they are corresponding angles due to their parallel lines. With that same concept, since BC and DE are parallel, angles 3 and 6 are also congruent. We already figured out that angle 3 is 45, therefore 6 is also 45.

Now that we know angle 6, we subtract it from 180 to get angle 7:

180-45=135

Angle 7 is 135.

Answer 2

Given :

`m\angle1=55\text{ and AB}\parallel CD\text{ and }BC\parallel DE`

`\angle\text{CDE}=90^o`

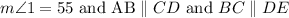
DC is a transversal line for the BC||DE.

`m\angle4\text{ and }\angle CDE\text{ are alternate interior angles.}`

We know that the alternate interior angles are equal.

`m\angle4=90^o`

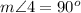
BC is a transversal line for the AB||CD.

`m\angle4\text{ and }\angle2\text{ are alternate interior angles.}`

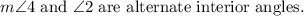
The alternate interior angles are equal.

`m\angle4=m\angle2=90^o`

Consider the triangle ABC.

By using the triangle sum property, we get

`m\angle1+m\angle2+m\angle3=180^o`
`\text{ Substitute }m\angle1=55\text{ and m}\angle2=90,\text{ we get}`

`55+90+m\angle3=180^o`

`55+90+m\angle3=180^o`