Adding 6x to the first equation we get:
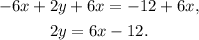
Dividing the above equation by 2 we get:
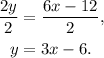
Now, adding 3x to the second equation we get:

Notice that both equations are equivalents.
Now, recall that to graph a line we only need 2 points on the line.
Substituting x=0 and x=1 at y=3x-6 we get:
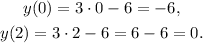
Then, both equations pass through the points (0,-6) and (2,0).
The graph of both equations is:
Since both graphs are the same line, the given system of equations has infinitely many solutions.
Answer:
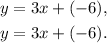
Infinite Number of solutions.