Question

Solve the following system of linear equations by graphing -6x+2y=-12-3x+y=-6

Answer 1

Adding 6x to the first equation we get:

`\begin{gathered} -6x+2y+6x=-12+6x, \\ 2y=6x-12. \end{gathered}`

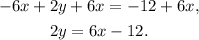
Dividing the above equation by 2 we get:

`\begin{gathered} (2y)/(2)=(6x-12)/(2), \\ y=3x-6. \end{gathered}`

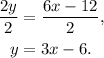
Now, adding 3x to the second equation we get:

`\begin{gathered} -3x+y+3x=-6+3x, \\ y=3x-6. \end{gathered}`

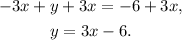
Notice that both equations are equivalents.

Now, recall that to graph a line we only need 2 points on the line.

Substituting x=0 and x=1 at y=3x-6 we get:

`\begin{gathered} y(0)=3\cdot0-6=-6, \\ y(2)=3\cdot2-6=6-6=0. \end{gathered}`

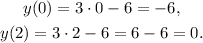
Then, both equations pass through the points (0,-6) and (2,0).

The graph of both equations is:

Since both graphs are the same line, the given system of equations has infinitely many solutions.

Answer:

`\begin{gathered} y=3x+(-6), \\ y=3x+(-6)\text{.} \end{gathered}`

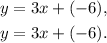
Infinite Number of solutions.